Manejo de data.phrames en lenguaje R

 i. Cree un script T5iniciales.R en R-Studio

ii. Ejecute la función data() desde la plataforma R-STUDIO e importe los conjuntos de datos trees

y npk de R; luego cree dos nuevos objetos data.frame df.arboles y df.npk; y traduzca el nombre

las columnas (variables) de ambos objetos.

iii. Para cada data frame creado, realice un análisis exploratorio de las variables respuesta (boxplots,

histogramas, frecuencias, summary, etc) considere los conjuntos de datos completos. Exporte sus

gráficas.

Para el conjunto de datos datos.npk,

iv. Calcule las medias y desviaciones estándar por bloque; cree dos subconjuntos de datos, uno para

todos los bloques pares y otro para todos los bloques nones.

Para el conjunto de datos datos.arboles,

v. Grafique por pares de variables; efectúe regresiones lineales entre el volumen (variable

dependiente) y (altura, perímetro) variables independientes; grafique los valores predichos

(ajustados) y los valores observados, exporte sus gráficas.

vi. Exporte los conjuntos de datos, datos.arboles y datos.npk a archivos .csv

vii. Exporte los valores predichos, observados y los residuales da cada modelo a un archive .csv.

viii. Genere 40 datos de peso de borregos con una media de 24 kg y sd de 5 kg (asuma normalidad).

Genere 40 datos de diámetro de cintura de borregos en cm con media 45 cm y sd 8 cm (asuma

normalidad). Grafique los datos peso (variable respuesta) vs diametro (variable predictora).

Efectúe una regresión lineal, analice y guarde sus resultados en archivos en forma ordenada y

comente sus resultados.

ix. Cree 3 pares de objetos tmin1, tmax1, tmin2, tmax2, tmax3, tmin3, de longitud 6, donde tmin son

temperaturas mínimas diarias y tmax son temperaturas máximas diarias. Luego utilice la función

tpromedio descrita en script de clase para calcular los promedios de temperatura tp1, tp2, tp3,

utilice el ciclo for para hacer el cálculo en forma iterativa.

x. Exporte a un archivo .RData el área de trabajo completa.

xi. Comente sus resultados en general.

#recupera algunas bases de datos y las hace objeto

data()

data(trees)

df.arboles <- trees

data(npk)

df.npk <- npk

#traduce los nombres de las columnas en cada df

names(df.arboles) <- c("perimetro", "altura", "volumen")

names(df.npk) <- c("bloque", "N", "P", "K", "campo")

#analisis exploratorio del df de arboles

cor(df.arboles$perimetro, df.arboles$volumen)

plot(df.arboles$volumen ~ df.arboles$perimetro, xlab = "Perimetro", 

         ylab = "Volumen", main = "Volumen de los arboles respecto a su perimetro")

hist(x = df.arboles$altura, xlab = "Altura", ylab = "Frecuencia", 

     main = "Frecuencia de arboles de acuerdo a su altura")

summary(df.arboles)

#analisis exploratorio del df de npk

boxplot(df.npk$campo ~ df.npk$bloque, xlab = "Bloque", 

        ylab = "Campo", main = "Comportamiento del campo con diferentes tratamientos de NPK")

hist(x = df.npk$campo, xlab = "Campo", ylab = "Frecuencia", 

     main = "Frecuencia del comportamiento del campo ante diferentes tratamientos")

summary(df.npk)

#para el conjunto de datos npk se calcula la media y la des. estandar por bloques

#ademas se obtienen subconjuntos de los bloques pares e impares

df.npk.media <- tapply(df.npk$campo, df.npk$bloque, mean)

df.npk.media

df.npk.sd <- tapply(df.npk$campo, df.npk$bloque, sd)

df.npk.sd

df.npk.subset.par <- subset(df.npk, df.npk$bloque == 2 | df.npk$bloque == 4 | df.npk$bloque == 6)

df.npk.subset.par

df.npk.subset.nones <- subset(df.npk, df.npk$bloque == 1 | df.npk$bloque == 3 | df.npk$bloque == 5)

df.npk.subset.nones

#para el conjunto de datos de arboles se obtienen regresiones lineales y graficas

df.arboles.reg1 <- lm(df.arboles$volumen ~ df.arboles$perimetro)

df.arboles.reg1

summary(df.arboles.reg1)

df.arboles.reg2 <- lm(df.arboles$volumen ~ df.arboles$altura)

df.arboles.reg2

summary(df.arboles.reg2)

plot(df.arboles$volumen ~ df.arboles$perimetro, xlab = "Perimetro", ylab = "Volumen",

     main = "Volumen de los arboles respecto a su perimetro")

plot(df.arboles$volumen ~ df.arboles$altura, xlab = "Altura", ylab = "Volumen",

     main = "Volumen de los arboles respecto a su altura")

#exporta los df creados

write.csv(df.arboles, file = "T5HJBVdf.arboles.csv")

write.csv(df.npk, file = "T5HJBVdf.npk.csv")

#crea objetos a partir de los modelos hechos y los exporta 

df.arboles.mod1 <- cbind(df.arboles$volumen, df.arboles$perimetro, df.arboles.reg1$residuals)

df.arboles.mod1

df.arboles.mod2 <- cbind(df.arboles$volumen, df.arboles$altura, df.arboles.reg2$residuals)

df.arboles.mod2

write.csv(df.arboles.mod1, file = "T5HJBVdf.arboles.mod1.csv")

write.csv(df.arboles.mod2, file = "T5HJBVdf.arboles.mod2.csv")

#analisis de algunas variables de borregos 

peso.bor <- rnorm(40, mean = 24, sd = 5)

peso.bor 

cintura.bor <- rnorm(40, mean = 45, sd = 8)

cintura.bor

plot(peso.bor ~ cintura.bor, xlab = "Diametro", ylab = "Peso", 

     main = "Peso de borregos de acuerdo a su diametro")

bor.reg <- lm(peso.bor ~ cintura.bor)

bor.reg

summary(bor.reg)

#analisis de temperaturas

i <- NULL; tp1 <- NULL; suma1 <- NULL

for(i in 1:6){

  tmin1 <- rnorm(1, mean = 14, sd = 2)

  tmax1 <- rnorm(1, mean = 27, sd = 2)

  tp1 <- (tmin1 + tmax1)/2;

  suma1 <- c(suma1, tp1);

}

suma1

tp1 <- sum(suma1)/6

tp1

i <- NULL; tp2 <- NULL; suma2 <- NULL

for(i in 1:6){

  tmin2 <- rnorm(1, mean = 16, sd = 2)

  tmax2 <- rnorm(1, mean = 29, sd = 2)

  tp2 <- (tmin2 + tmax2)/2;

  suma2 <- c(suma2, tp2);

}

suma2

tp2 <- sum(suma2)/6

tp2

i <- NULL; tp3 <- NULL; suma3 <- NULL

for(i in 1:6){

  tmin3 <- rnorm(1, mean = 16, sd = 2)

  tmax3 <- rnorm(1, mean = 29, sd = 2)

  tp3 <- (tmin3 + tmax3)/2;

  suma3 <- c(suma3, tp3);

}

suma3

tp3 <- sum(suma3)/6

tp3

 

·         Análisis exploratorio

En el análisis exploratorio del conjunto de datos sobre árboles se obtuvieron las gráficas de la figura 1 y la figura 2. En la figura 1 se ve la relación que tienen las variables perímetro y volumen, que son directamente proporcional.

Figura 1. Relación entre las variables perímetro y volumen. Fuente: propia

En la figura 2 se puede apreciar un histograma de la variable altura de los árboles. Los arboles con altura entre 75 y 80 unidades se distinguen por ser lo más numerosos.

Figura 2. Histograma de la variable altura de los árboles. Fuente: propia.

Por el otro lado, el análisis exploratorio de los datos sobre NPK se ilustran en las gráficas de las figuras 3 y 4. En la figura 3, se aprecia un boxplot entre las variables bloque y campo. Se observa un mejor rendimiento en el bloque 3 por encima de los otros bloques.

Figura 3. Boxplot de las variables bloque y campo. Fuente: propia.

En la figura 4 se ilustra el histograma de la variable campo. Se aprecia que el mejor rendimiento se dio entre 55 a 60 unidades.

Figura 4. Histograma de la variable campo. Fuente: propia.

 

 

·         Regresiones lineales entre las variables de los datos sobre arboles

Como se comentó con anterioridad, el perímetro y el volumen de los arboles tienen una relación directamente proporcional con un R² de 0.93. El modelo que representa esta relación es:  

y=5.066x-36.943

Figura 5. Regresión lineal entre las variables volumen y perímetro. Fuente: propia.

La relación entre la altura y el volumen de los arboles no es muy alta con un R² de 0.34. El modelo que representa esta relación es:

y=1.543x-87.124

Figura 6. Regresión lineal entre las variables volumen y altura. Fuente: propia.

·         Análisis de los datos de cintura y peso de borregos

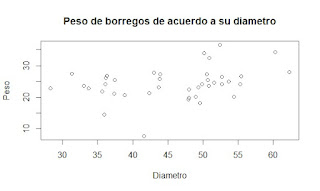
En la figura 7 se observa la gráfica de los datos del diámetro de la cintura de borregos con su respectivo peso. Estos datos se obtuvieron al azar de acuerdo a algunos criterios de media y desviación estándar. Se observa que los datos no tienen una relación con un R² de 0.07. El modelo que representa esta relación es: y=0.1933x+15.4369

 

Figura 7. Regresión lineal entre la cintura y el peso de borregos. Fuente: propia.