1. y''+4y=x y(0)=1,y'(0)=0
2. y''-y=sinx y(0)=0,y'(0)=-1/2
3. y''-y'-2y=x+1 y(0)=0,y'(0)=0
4. y''-2y'+y=e^x y(0)=0,y'(0)=1
5. y''-3y'+2y=sinhx y(0)=0,y'(0)=0
6. y''+y'=x y(0)=1,y'(0)=1
7. y''+y=x-e^x y(0)=0,y'(0)=0
8. y''-2y'=xe^x y(0)=-1,y'(0)=0
9. y''-4y'+3y=cosx y(0)=1,y'(0)=-1
10. y''+2y'+2y=x-e^(-x) y(0)=0,y'(0)=0
jueves, 26 de diciembre de 2013
ECUACIONES DIFERENCIALES. VARIABLES SEPARABLES, CAMBIO DE VARIABLE, ECUACIONES DIFERENCIALES EXACTAS
En está publicación encontraran la solución de los siguientes ejercicios:
Variables separables:
1. (dy/dx) =(b^2x)/(a^2y)
2. x^3 (dy/dx) +y^2=0
3. (dy/dx) =senx/cosy
4. (dy/dx)=y/2x
5. (dy/dx)=e^(-y)cosx
6. xy+y^2(dy/dx)=6x
7. xydx-(x+2)dy=0
8. (xy+x)dx=(x^2y^2+x^2+y^2+1)dy
9. (dy/dx)+((1-y^2)/(1-x^2))^2=0
10. ylnxlnydx+dy=0
Cambio de variable:
11. (dy/dx)=tan(x+y)
12. (dy/dx)=1/(ln(2x+y+3)+1)-2
13. (dy/dx)=e^(x+y-1)-1
14. (dy/dx)=sen(x+y)
15. (dy/dx)=x^2+y-1
Otros:
1. 3x^2(dy/dx)=2x^2+y^2
2. xydx-(x^2+2y^2)dy=0
3. (raíz(x^2-y^2)-yarcsen(y/x))dx=-xarcsen(y/x)dy
Ecuaciones diferenciales exactas:
1. (2x-1)dx+(3y+7)dy=0
2. (2x+y)dx+(-x-6y)dy=0
3. (5x+4y)dx+(4x-8y^3)dy=0
4. (seny-ysenx)dx+(cosx+xcosy)dy=0
5. (2xy^2-3)dx+(2x^2y+4)dy=0
6. (2y-1/x+cos3x)(dy/dx)+y/x^2-4x^3+3ysen3x=0
7. (x^2-y^2)dx+(x^2-2xy)dy=0
8. (1+lnx+y/x)dx=(1-lnx)dy
9. (x-y^3+y^2senx)dx=(3xy^2+2ycosx)dy
10. (x^3+y^3)dx+3xy^2dy=0
11. (ylny-e^(-xy))dx+(1/y+xlny)dy=0
12. (3x^2y+e^y)dx+(x^3+xe^y-2y)dy=0
13. x(dy/dx)=2xe^x-y+6x^2
14. (1-3/y+x)(dy/dx)+y=3/x-1
15. (x^2y^3-1/(1+9x^2))(dy/dx)+x^3y^2=0
16. (5y-2x)y'-2y=0
17. (tanx-senx seny)dx+cosxcosydy=0
18. (2ysenxcos-y+2y^2e^(xy^2))dx=(x-sen^2x-4xye^(xy^2))dy
19. (4t^3y-15t^2-y)dt+(y^4+3y^2-t)dy=0
20. (1/t+1/t^2-y/(t^+y^2))dt+(ye^y+t/(t^2+y^2))dy=0
Variables separables:
1. (dy/dx) =(b^2x)/(a^2y)
2. x^3 (dy/dx) +y^2=0
3. (dy/dx) =senx/cosy
4. (dy/dx)=y/2x
5. (dy/dx)=e^(-y)cosx
6. xy+y^2(dy/dx)=6x
7. xydx-(x+2)dy=0
8. (xy+x)dx=(x^2y^2+x^2+y^2+1)dy
9. (dy/dx)+((1-y^2)/(1-x^2))^2=0
10. ylnxlnydx+dy=0
Cambio de variable:
11. (dy/dx)=tan(x+y)
12. (dy/dx)=1/(ln(2x+y+3)+1)-2
13. (dy/dx)=e^(x+y-1)-1
14. (dy/dx)=sen(x+y)
15. (dy/dx)=x^2+y-1
Otros:
1. 3x^2(dy/dx)=2x^2+y^2
2. xydx-(x^2+2y^2)dy=0
3. (raíz(x^2-y^2)-yarcsen(y/x))dx=-xarcsen(y/x)dy
Ecuaciones diferenciales exactas:
1. (2x-1)dx+(3y+7)dy=0
2. (2x+y)dx+(-x-6y)dy=0
3. (5x+4y)dx+(4x-8y^3)dy=0
4. (seny-ysenx)dx+(cosx+xcosy)dy=0
5. (2xy^2-3)dx+(2x^2y+4)dy=0
6. (2y-1/x+cos3x)(dy/dx)+y/x^2-4x^3+3ysen3x=0
7. (x^2-y^2)dx+(x^2-2xy)dy=0
8. (1+lnx+y/x)dx=(1-lnx)dy
9. (x-y^3+y^2senx)dx=(3xy^2+2ycosx)dy
10. (x^3+y^3)dx+3xy^2dy=0
11. (ylny-e^(-xy))dx+(1/y+xlny)dy=0
12. (3x^2y+e^y)dx+(x^3+xe^y-2y)dy=0
13. x(dy/dx)=2xe^x-y+6x^2
14. (1-3/y+x)(dy/dx)+y=3/x-1
15. (x^2y^3-1/(1+9x^2))(dy/dx)+x^3y^2=0
16. (5y-2x)y'-2y=0
17. (tanx-senx seny)dx+cosxcosydy=0
18. (2ysenxcos-y+2y^2e^(xy^2))dx=(x-sen^2x-4xye^(xy^2))dy
19. (4t^3y-15t^2-y)dt+(y^4+3y^2-t)dy=0
20. (1/t+1/t^2-y/(t^+y^2))dt+(ye^y+t/(t^2+y^2))dy=0
ECUACIONES DIFERENCIALES. MODELADO CON ECUACIONES DIFERENCIALES DE PRIMER ORDEN
Crecimiento y
decrecimiento:
1. Se sabe que la población de una
comunidad crece con una razón proporcional al número de personas presentes en
el tiempo t. Si la población inicial P0 se duplicó en 5 años, ¿En
cuánto tiempo se triplicará y cuadruplicará?
t=10.0021 años
La
población se triplicara a los 7.9265
10.0021 años.
2.
La población de un pueblo crece con una razón
proporcional a la población en el tiempo t. La población inicial de 500
aumenta 15% en 10 años. ¿Cuál será la población pasados 30 años? ¿Qué tan
rápido está creciendo la población en t = 30?
3.
El isótopo radiactivo del plomo Pb-209, decae
con una razón proporcional a la cantidad presente al tiempo t y tiene un
vida media de 3.3 horas. Si al principio había 1 gramo de plomo, ¿cuánto tiempo
debe transcurrir para que decaiga 90%?
4. Cuando pasa un rayo vertical de luz
por un medio transparente, la razón con que decrece su intensidad I es
proporcional a I(t), donde t representa el espesor, en
pies, del medio. En agua limpia de mar, la intensidad a 3 pies debajo de la
superficie es 25% de la intensidad inicial I0 del rayo incidente. ¿Cuál
es la intensidad del rayo a 15 pies debajo de la superficie?
Ley de Newton
enfriamiento/calentamiento:
1.
Un termómetro se cambia de una habitación
donde la temperatura es de 70° F al exterior, donde la temperatura del aire es
de 10° F. Después de medio minuto el termómetro indica 50° F. ¿Cuál es la
lectura del termómetro en t =1 min? ¿Cuánto tiempo le tomará al
termómetro alcanzar los 15° F?
2.
Una pequeña barra de metal, cuya temperatura
inicial era de 20° C, se deja caer en un gran tanque de agua hirviendo. ¿Cuánto
tiempo tardará la barra en alcanzar los 90° C si se sabe que su temperatura
aumentó 2° en 1 segundo? ¿Cuánto tiempo tardará en alcanzar los 98° C?
3. Un termómetro que indica 70° F se
coloca en un horno precalentado a una temperatura constante. A través de una
ventana de vidrio en la puerta del horno, un observador registra que el
termómetro lee 110° F después de ½ minuto y 145° F después de 1 minuto. ¿Cuál
es la temperatura del horno?
4. Un cadáver se encontró dentro de un
cuarto cerrado en una casa donde la temperatura era constante a 70° F. Al
tiempo del descubrimiento la temperatura del corazón del cadáver se determinó
de 85° F. Una hora después una segunda medición mostró que la temperatura del
corazón era de 80° F. Suponga que el tiempo de la muerte corresponde a t =
0 y que la temperatura del corazón en ese momento era de 98.6° F. Determine
¿cuántas horas pasaron antes de que se encontrara el cadáver? [Sugerencia:
Sea que t1 > 0 denote el tiempo en que se encontró el cadáver.]
Mezclas:
1.
Un tanque contiene 200 litros de un
líquido en el que se han disuelto 30 g de sal. Salmuera que tiene 1 g de sal
por litro entra al tanque con una razón de 4 L/min; la solución bien mezclada
sale del tanque con la misma razón. Encuentre la cantidad A(t) de
gramos de sal que hay en el tanque al tiempo t.
3.
Un gran tanque está parcialmente lleno con
100 galones de fluido en los que se disolvieron 10 libras de sal. La sal- muera
tiene ½ de sal por galón que entra al tanque a razón de 6 gal/min. La solución
bien mezclada sale del tanque a razón de 4 gal/min. Determine la cantidad de
libras de sal que hay en el tanque después de 30 minutos.
ECUACIONES DIFERENCIALES. SERIES DE POTENCIA
* 2y''+xy'+y=0 x0=1
* y''-xy=0 x0=0
* y''+x^2y=0 x0=0
* y''-2xy'+y=0 x0=0
* y''-xy'+2y=0 x0=0
* y''-x^2y'+xy=0 x0=0
* y''+2xy'+2y=0 x0=0
* (x-1)y''+y'=0 x0=0
* (x+2)y''+xy'-y=0 x0=0
* y''-(x-1)y'-y=0 x0=0
* (x^2-+)y''-6y=0 x0=0
MECANICA DE FLUIDOS. TUBERÍAS EN SERIE (Ejercicios Robert Mott )
or el sistema que se ilustra en la figura 11.11 circula agua a 10 °C que proviene de un almacenamiento grande, a razón de 1.5 X 10^-2 m /s. Calcule la presión en el punto B.
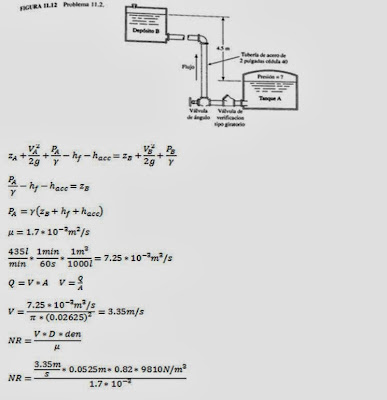
Por el sistema de la figura 11.12 va a forzarse la circulación
de keroseno (sg = 0.82) a 20 ’C del tanque A al deposito B,
por medio del incremento de la presión sobre
el keroseno que se encuentra en el tanque A, sellado
La longitud total de la tubería de acero de 2 pulga
as cédula 40 es de 38 m. El codo es estándar. Calcule
la presión que se requiere en el tanque A pora ocasionar
un flujo volumétrico de 435 L/min.
A travcés del sistema de la figura 11.17 fluye líquido
refrigerante a razón de 1.70 L/min. El refrigerante tiene
una gravedad especifica de 1,25 y viscocidad dinámica
de 3 \ 10^ -4 Pa-s. Calcule la diferencia de presion
entre los puntos A y B. El tubo está hecho de acero, con
diámetro externo de 1/2 pulgada, espesor de pared de
0.04 pulgada y longitud total de 30 m
Suscribirse a:
Entradas (Atom)